Design and Analysis of Algorithms
Design and Analysis of Algorithm is very important for designing algorithm to solve different types of problems in the branch of computer science and information technology.
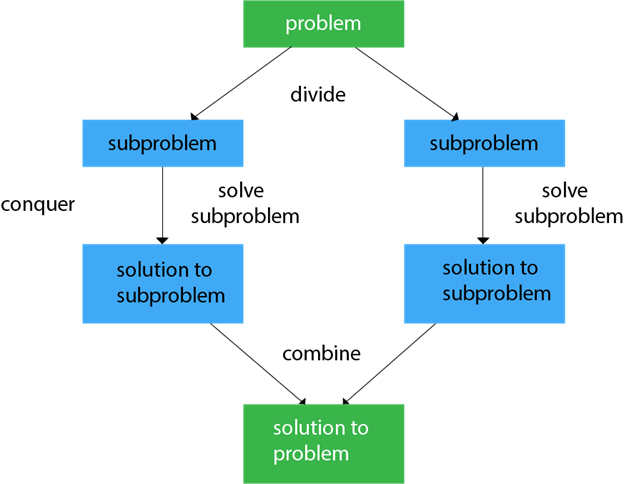
Divide and Conquer
Divide and Conquer algorithm consists of three steps. Divide the problem into a set of subproblems. Conquer: Solve every subproblem individually, recursively. Combine: Put together the solutions of the subproblems to get the whole solution

Dynamic Programming
Dynamic Programming solves problems by combining the solutions of subproblems. It solves each sub-problem just once and then saves its answer in a table, thereby avoiding the work of re-computing the answer every time.

Branch and Bound
Branch and bound is an algorithm design paradigm which is generally used for solving combinatorial optimization problems.It solves these problems relatively quickly.
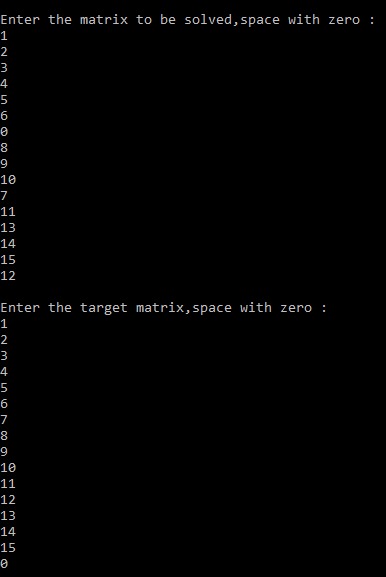
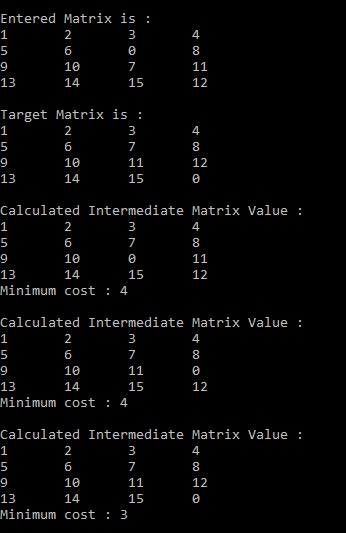
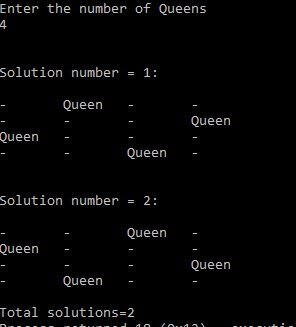
Backtracking
Backtracking is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time

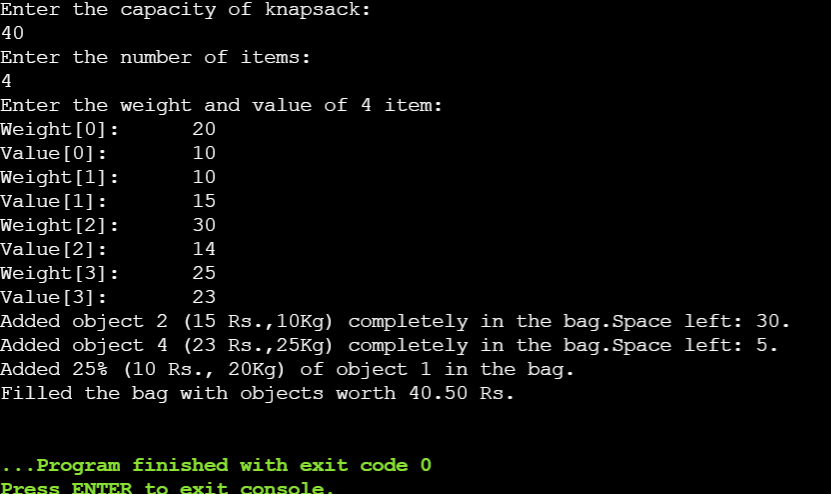
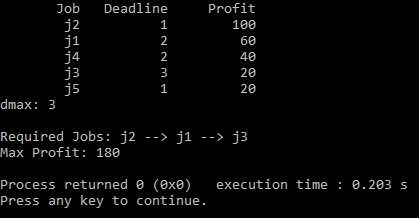
Greedy Method
A greedy algorithm is a simple, intuitive algorithm that is used in optimization problems. The algorithm makes the optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem.

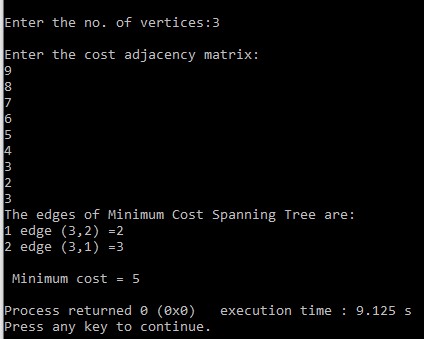
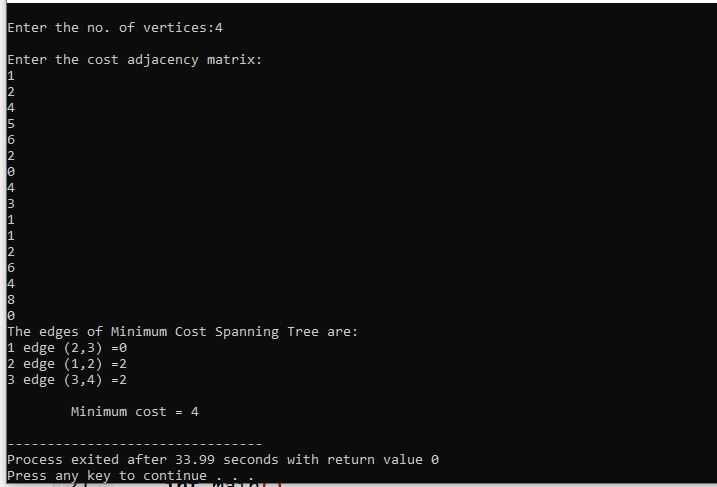
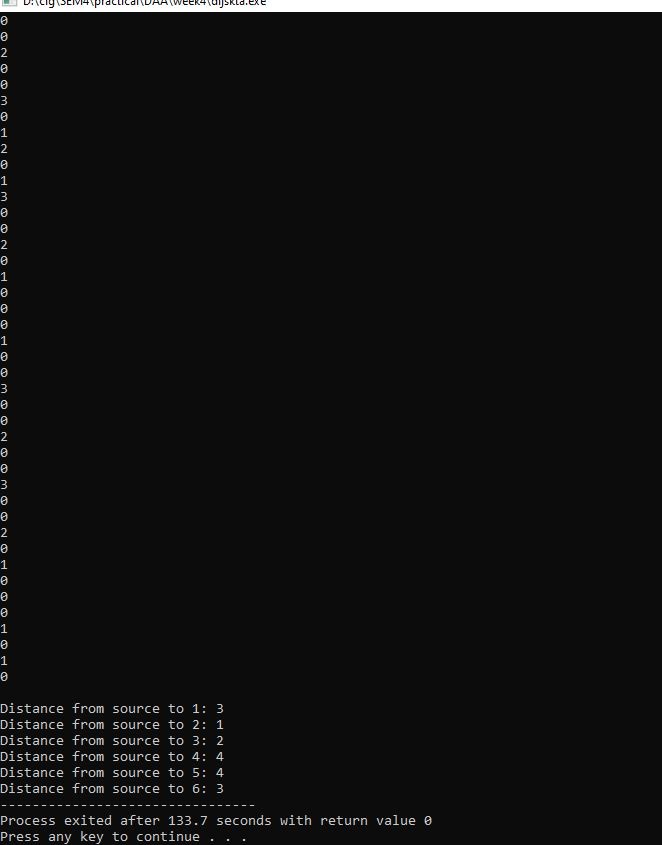
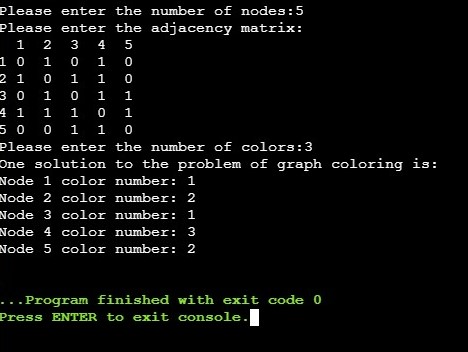
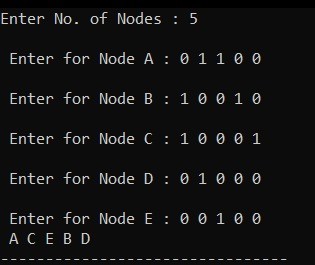
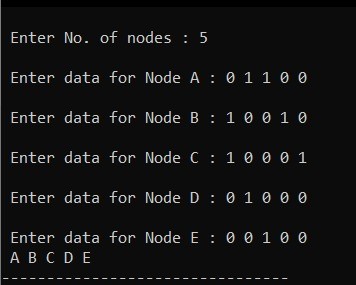
Graph Traversal algorithm
Graph traversal is a technique used for a searching vertex in a graph. The graph traversal is also used to decide the order of vertices is visited in the search process. A graph traversal finds the edges to be used in the search process without creating loops.