Data Structures & Algorithms

ALGORITHM

• 1. If(M < N) then BACK=M+1 else STOP
• 2. While (BACK>i) repeat steps 3 to 4
• 3. REG[BACK]= REG[BACK-1]
• 4. BACK=BACK-1;
• 5. Reg[BACK]='X'
• 6. M=M+1
• 7. End.
          

CODE

#include<stdio.h>
int main()
{
int arr[10],n,i,pos,num;
printf("enter how many elements in the array = ");
scanf("%d",&n);
printf("enter the elements in the array = \n");
for(i=0;i< n;i++)
{
scanf("%d",&arr[i]);
}
printf("the elements in the array is = \n");
for(i=0;i< n;i++)
printf("arr[%d]= %d\n",i,arr[i]);
printf("\n\n");
printf("enter the number to be inserted = ");
scanf("%d",&num);
printf("enter the place where to be inserted = ");
scanf("%d",&pos);
for(i=n-1;i>=pos;i--)
{
    arr[i+1]=arr[i];
}
arr[pos]=num;
n= n+1;
printf("the new array is = \n");
for(i=0;i< n;i++)
    printf("arr[%d] = %d\n",i,arr[i]);
}
  

TIME COMPLEXITY

O(N)

EXPLANATION

OUTPUT

ALGORITHM

1. Back=1
2. While (Back < M) repeat 3 and 4
3. Reg[Back]=Reg[Back+1]
4. Back= Back+1
5. M=M-1
6. End


          

CODE

#include<stdio.h>
int main()
{
int n,i,pos,arr[10];
printf("enter the number of elements in the array = \n");
scanf("%d",&n);
printf("enter the elements in the array = \n");
for(i=0;i< n;i++)
{
scanf("%d",&arr[i]);
}
printf("the elements in the array = \n");
for(i=0;i< n;i++)
{
printf("arr[%d] = %d\n",i,arr[i]);
}
printf("enter the position element to delete = ");
scanf("%d",&pos);
for(i=pos;i< n-1;i++)
{
    arr[i]=arr[i+1];
}
n=n-1;
printf("the new array is = \n");
for(i=0;i< n;i++)
printf("arr[%d] = %d\n",i,arr[i]);
}

  

TIME COMPLEXITY

O(N)

EXPLANATION

OUTPUT

ALGORITHM

We first define a stack of max size
PUSH(): First, we check if the stack is full, if the top pointing is equal to (MAX-1), it means that stack is full and no more elements can be inserted we print overflow. Otherwise, we increment the top variable and store the value to the index pointed by the top variable 

POP(): First, we check if the stack is empty, if the top variable has a value less than 0, it means the stack is empty. So, we can't delete any more elements and print underflow condition. Otherwise, we decrement the top variable.

PEEK(): The PEEK() function returns the topmost value stored in stack, it's done by returning the element pointed by the top variable.

          

CODE

#include<stdio.h>
#define N 5
int stack[N];
int top = -1;
void push()
{
int x;
printf("enter the element to push = ");
scanf("%d",&x);
if(top == N-1)
printf("stack is full\n ");
else
{
top++;
stack[top] = x;
}
}
void pop()
{
int y;
if(top==-1)
printf("stack is empty\n");
else
{
y= stack[top];
top--;
printf("%d will be pooped\n",y);
}
}
void peek()
{
if(top==-1)
printf("the stack is empty\n");
else
printf("%d is the topmost element in the stack\n",stack[top]);
}
void display()
{
int i;
for(i=top;i>=0;i--)
{
printf("%d is in the stack\n",stack[i]);
}
}
int main()
{
int z;
while(1)
{
printf("enter your choice : 1-push: 2-pop: 3-peek: 4-display\n");
printf("enter your choice = ");
scanf("%d",&z);
switch(z)
{
case 1:push();break;
case 2:pop();break;
case 3:peek();break;
case 4:display();break;
default:printf("invalid status\n");
}
}
}
                
  

TIME COMPLEXITY

pop-O(1)

push-O(1)

top-O(1)

isEmpty-O(1)

Access-O(n)

Search-O(n) 

EXPLANATION

OUTPUT

ALGORITHM

1.We first create a node with value Null.


2.Then when we have to push an element new we check if new is not null otherwise insertion cannot be done. We then feed Item into data part of new and assign top to its link and top is updated to the new value. And thus, an element is inserted.


3.For popping we check first if the item is not null, otherwise stack is empty i.e underflow condition. The pointer is then made to point the next element and st_head link is assigned to the pointer's value. This eliminates the element from the link list. Thus, popping the element


4.Peek value is stored or printed by returning node at which top is pointing

5.Stop
          

CODE

# include<stdio.h>
# include<stdlib.h>
# include<string.h>
static int i=0;
typedef struct List
  {
  char data[20];
  struct List* next;
  }Node;

Node* push(Node *top)
  {
  Node *new;
  new=(Node*)malloc(sizeof(Node));
  printf("\nEnter data : ");
  scanf("%s",new->data);
  new->next=top;
  top=new;
  return top;
  }
  
Node* pop(Node *top)
{
  Node * ptr;
  if(top==NULL)
    {
    printf("\nStack Underflow!!!");
    return top;
    }
  ptr=top;
  top=ptr->next;
  if(ptr!=NULL)
  {
    printf("\n%s popped out of Stack",ptr->data);
    ptr->next=NULL;
    free (ptr);
  }
  return top;
}

void display(Node *ptr)
{
  
  if((ptr==NULL)&&(i==0))
  {
    printf("\nStack Empty!!!\nNothing to display");
    return;
  }
  if(ptr==NULL)
  {
    return;
  }
  i++;
  if(i==1)			
  printf("\n| ");
  display(ptr->next);
  printf("%s | ",ptr->data);
  
  
  
  return;
}


void main()
{
  int ch,l;
  float f;
  Node *top;
  top=NULL;
  
  while(1)
  {
  printf("\n1. Push");
  printf("\n2. Pop");
  printf("\n3. Display");
  printf("\n4. Exit");
  printf("\nEnter your choice : ");
  scanf("%d",&ch);
  switch(ch)
  {
    case 1:
    top=push(top);
    break;
    
    case 2:
    top=pop(top);
    break;
    
    case 3:
    i=0;
    display(top);
    break;
    
    case 4:
    if(top!=NULL)
      while(top!=NULL)
      {
        Node *ptr=top;
        free (ptr);
        top=top->next;
      }
    display(top);
    printf("\n");
      
    exit(0);
    
    default:
    printf("\nWrong choice !!!");
  }
  }
}
                
  

TIME COMPLEXITY

  The time complexity for all push(), pop(), and peek() operations is O(1)  

EXPLANATION

OUTPUT

ALGORITHM

Step 1 : Scan the Infix Expression from left to right.
Step 2 : If the scanned character is an operand, append it with final Infix to Postfix string.
Step 3 : Else,
Step 3.1 : If the precedence order of the scanned(incoming) operator is greater than the precedence order of the operator in the stack (or the stack is empty or the stack contains a ‘(‘ or ‘[‘ or ‘{‘), push it on stack.
Step 3.2 : Else, Pop all the operators from the stack which are greater than or equal to in precedence than that of the scanned operator. After doing that Push the scanned operator to the stack. (If you encounter parenthesis while popping then stop there and push the scanned operator in the stack.)
Step 4 : If the scanned character is an ‘(‘ or ‘[‘ or ‘{‘, push it to the stack.
Step 5 : If the scanned character is an ‘)’or ‘]’ or ‘}’, pop the stack and and output it until a ‘(‘ or ‘[‘ or ‘{‘ respectively is encountered, and discard both the parenthesis.
Step 6 : Repeat steps 2-6 until infix expression is scanned.
Step 7 : Print the output
Step 8 : Pop and output from the stack until it is not empty.
          

CODE

#include<stdio.h>
#include<stdlib.h>      /* for exit() */
#include<ctype.h>     /* for isdigit(char ) */
#include<string.h>

#define SIZE 100


/* declared here as global variable because stack[]
* is used by more than one fucntions */
char stack[SIZE];
int top = -1;

/* define push operation */

void push(char item)
{
  if(top >= SIZE-1)
  {
    printf("\nStack Overflow.");
  }
  else
  {
    top = top+1;
    stack[top] = item;
  }
}

/* define pop operation */
char pop()
{
  char item ;

  if(top < 0)
  {
    printf("stack under flow: invalid infix expression");
    getchar();
    /* underflow may occur for invalid expression */
    /* where ( and ) are not matched */
    exit(1);
  }
  else
  {
    item = stack[top];
    top = top-1;
    return(item);
  }
}

/* define function that is used to determine whether any symbol is operator or not
(that is symbol is operand)
* this fucntion returns 1 if symbol is opreator else return 0 */

int is_operator(char symbol)
{
  if(symbol == '^' || symbol == '*' || symbol == '/' || symbol == '+' || symbol =='-')
  {
    return 1;
  }
  else
  {
  return 0;
  }
}

/* define fucntion that is used to assign precendence to operator.
* Here ^ denotes exponent operator.
* In this fucntion we assume that higher integer value
* means higher precendence */

int precedence(char symbol)
{
  if(symbol == '^')/* exponent operator, highest precedence*/
  {
    return(3);
  }
  else if(symbol == '*' || symbol == '/')
  {
    return(2);
  }
  else if(symbol == '+' || symbol == '-')          /* lowest precedence */
  {
    return(1);
  }
  else
  {
    return(0);
  }
}

void InfixToPostfix(char infix_exp[], char postfix_exp[])
{ 
  int i, j;
  char item;
  char x;

  push('(');                               /* push '(' onto stack */
  strcat(infix_exp,")");                  /* add ')' to infix expression */

  i=0;
  j=0;
  item=infix_exp[i];         /* initialize before loop*/

  while(item != '\0')        /* run loop till end of infix expression */
  {
    if(item == '(')
    {
      push(item);
    }
    else if( isdigit(item) || isalpha(item))
    {
      postfix_exp[j] = item;              /* add operand symbol to postfix expr */
      j++;
    }
    else if(is_operator(item) == 1)        /* means symbol is operator */
    {
      x=pop();
      while(is_operator(x) == 1 && precedence(x)>= precedence(item))
      {
        postfix_exp[j] = x;                  /* so pop all higher precendence operator and */
        j++;
        x = pop();                       /* add them to postfix expresion */
      }
      push(x);
      /* because just above while loop will terminate we have
      oppped one extra item
      for which condition fails and loop terminates, so that one*/

      push(item);                 /* push current oprerator symbol onto stack */
    }
    else if(item == ')')         /* if current symbol is ')' then */
    {
      x = pop();                   /* pop and keep popping until */
      while(x != '(')                /* '(' encounterd */
      {
        postfix_exp[j] = x;
        j++;
        x = pop();
      }
    }
    else
    { /* if current symbol is neither operand not '(' nor ')' and nor
      operator */
      printf("\nInvalid infix Expression.\n");        /* the it is illegeal  symbol */
      getchar();
      exit(1);
    }
    i++;


    item = infix_exp[i]; /* go to next symbol of infix expression */
  } /* while loop ends here */
  if(top>0)
  {
    printf("\nInvalid infix Expression.\n");        /* the it is illegeal  symbol */
    getchar();
    exit(1);
  }
  if(top>0)
  {
    printf("\nInvalid infix Expression.\n");        /* the it is illegeal  symbol */
    getchar();
    exit(1);
  }


  postfix_exp[j] = '\0'; /* add sentinel else puts() fucntion */
  /* will print entire postfix[] array upto SIZE */

}

/* main function begins */
int main()
{
  char infix[SIZE], postfix[SIZE];         /* declare infix string and postfix string */

  /* why we asked the user to enter infix expression
  * in parentheses ( )
  * What changes are required in porgram to
  * get rid of this restriction since it is not
  * in algorithm
  * */
  printf("ASSUMPTION: The infix expression contains single letter variables and single digit constants only.\n");
  printf("\nEnter Infix expression : ");
  gets(infix);

  InfixToPostfix(infix,postfix);                   /* call to convert */
  printf("Postfix Expression: ");
  puts(postfix);                     /* print postfix expression */

  return 0;
} 
  

TIME COMPLEXITY

  The time complexity of an infix to postfix expression conversion algorithm is mathematically found to be O(N)

EXPLANATION

OUTPUT

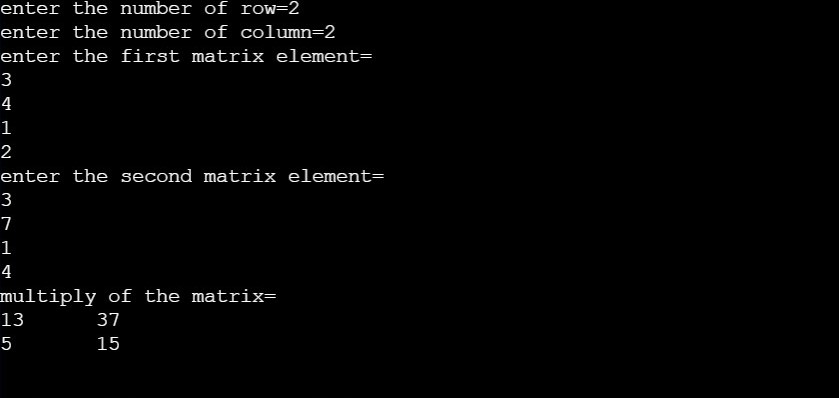
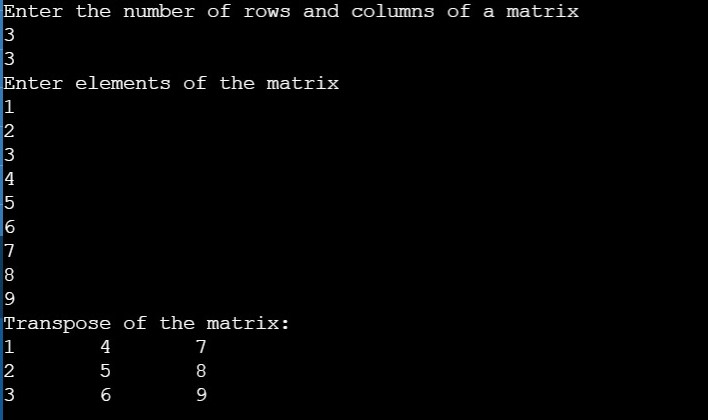
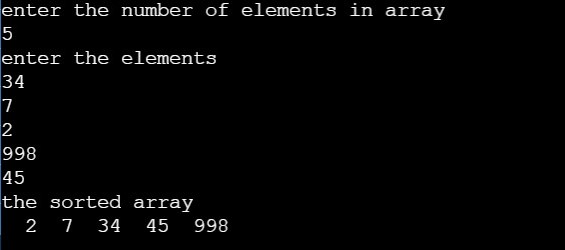
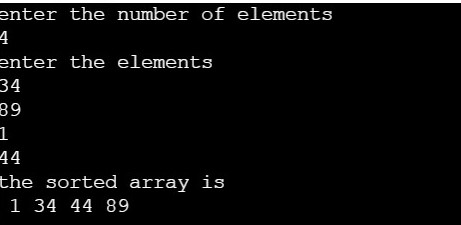
ALGORITHM

            Operations on Single Linked List
            The following operations are performed on a Single Linked List
            
            Insertion
            Deletion
            Display
            Before we implement actual operations, first we need to set up an empty list. First, perform the following steps before implementing actual operations.
            
            Step 1 - Include all the header files which are used in the program.
            Step 2 - Declare all the user defined functions.
            Step 3 - Define a Node structure with two members data and next
            Step 4 - Define a Node pointer 'head' and set it to NULL.
            Step 5 - Implement the main method by displaying operations menu and make suitable function calls in the main method to perform user selected operation.
            Insertion
            In a single linked list, the insertion operation can be performed in three ways. They are as follows...
            
            Inserting At Beginning of the list
            Inserting At End of the list
            Inserting At Specific location in the list
            Inserting At Beginning of the list
            We can use the following steps to insert a new node at beginning of the single linked list...
            
            Step 1 - Create a newNode with given value.
            Step 2 - Check whether list is Empty (head == NULL)
            Step 3 - If it is Empty then, set newNode→next = NULL and head = newNode.
            Step 4 - If it is Not Empty then, set newNode→next = head and head = newNode.
            Inserting At End of the list
            We can use the following steps to insert a new node at end of the single linked list...
            
            Step 1 - Create a newNode with given value and newNode → next as NULL.
            Step 2 - Check whether list is Empty (head == NULL).
            Step 3 - If it is Empty then, set head = newNode.
            Step 4 - If it is Not Empty then, define a node pointer temp and initialize with head.
            Step 5 - Keep moving the temp to its next node until it reaches to the last node in the list (until temp → next is equal to NULL).
            Step 6 - Set temp → next = newNode.
            Inserting At Specific location in the list (After a Node)
            We can use the following steps to insert a new node after a node in the single linked list...
            
            Step 1 - Create a newNode with given value.
            Step 2 - Check whether list is Empty (head == NULL)
            Step 3 - If it is Empty then, set newNode → next = NULL and head = newNode.
            Step 4 - If it is Not Empty then, define a node pointer temp and initialize with head.
            Step 5 - Keep moving the temp to its next node until it reaches to the node after which we want to insert the newNode (until temp1 → data is equal to location, here location is the node value after which we want to insert the newNode).
            Step 6 - Every time check whether temp is reached to last node or not. If it is reached to last node then display 'Given node is not found in the list!!! Insertion not possible!!!' and terminate the function. Otherwise move the temp to next node.
            Step 7 - Finally, Set 'newNode → next = temp → next' and 'temp → next = newNode'
            Deletion
            In a single linked list, the deletion operation can be performed in three ways. They are as follows...
            
            Deleting from Beginning of the list
            Deleting from End of the list
            Deleting a Specific Node
            Deleting from Beginning of the list
            We can use the following steps to delete a node from beginning of the single linked list...
            
            Step 1 - Check whether list is Empty (head == NULL)
            Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
            Step 3 - If it is Not Empty then, define a Node pointer 'temp' and initialize with head.
            Step 4 - Check whether list is having only one node (temp → next == NULL)
            Step 5 - If it is TRUE then set head = NULL and delete temp (Setting Empty list conditions)
            Step 6 - If it is FALSE then set head = temp → next, and delete temp.
            Deleting from End of the list
            We can use the following steps to delete a node from end of the single linked list...
            
            Step 1 - Check whether list is Empty (head == NULL)
            Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
            Step 3 - If it is Not Empty then, define two Node pointers 'temp1' and 'temp2' and initialize 'temp1' with head.
            Step 4 - Check whether list has only one Node (temp1 → next == NULL)
            Step 5 - If it is TRUE. Then, set head = NULL and delete temp1. And terminate the function. (Setting Empty list condition)
            Step 6 - If it is FALSE. Then, set 'temp2 = temp1 ' and move temp1 to its next node. Repeat the same until it reaches to the last node in the list. (until temp1 → next == NULL)
            Step 7 - Finally, Set temp2 → next = NULL and delete temp1.
            Deleting a Specific Node from the list
            We can use the following steps to delete a specific node from the single linked list...
            
            Step 1 - Check whether list is Empty (head == NULL)
            Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
            Step 3 - If it is Not Empty then, define two Node pointers 'temp1' and 'temp2' and initialize 'temp1' with head.
            Step 4 - Keep moving the temp1 until it reaches to the exact node to be deleted or to the last node. And every time set 'temp2 = temp1' before moving the 'temp1' to its next node.
            Step 5 - If it is reached to the last node then display 'Given node not found in the list! Deletion not possible!!!'. And terminate the function.
            Step 6 - If it is reached to the exact node which we want to delete, then check whether list is having only one node or not
            Step 7 - If list has only one node and that is the node to be deleted, then set head = NULL and delete temp1 (free(temp1)).
            Step 8 - If list contains multiple nodes, then check whether temp1 is the first node in the list (temp1 == head).
            Step 9 - If temp1 is the first node then move the head to the next node (head = head → next) and delete temp1.
            Step 10 - If temp1 is not first node then check whether it is last node in the list (temp1 → next == NULL).
            Step 11 - If temp1 is last node then set temp2 → next = NULL and delete temp1 (free(temp1)).
            Step 12 - If temp1 is not first node and not last node then set temp2 → next = temp1 → next and delete temp1 (free(temp1)).
            Displaying a Single Linked List
            We can use the following steps to display the elements of a single linked list...
            
            Step 1 - Check whether list is Empty (head == NULL)
            Step 2 - If it is Empty then, display 'List is Empty!!!' and terminate the function.
            Step 3 - If it is Not Empty then, define a Node pointer 'temp' and initialize with head.
            Step 4 - Keep displaying temp → data with an arrow (--->) until temp reaches to the last node
            Step 5 - Finally display temp → data with arrow pointing to NULL (temp → data ---> NULL).
            
          

CODE

#include<stdio.h>  
#include<stdlib.h>  
struct node   
{  
    int data;  
    struct node *next;   
};  
struct node *head;  
  
void beginsert ();   
void lastinsert ();  
void randominsert();  
void begin_delete();  
void last_delete();  
void random_delete();  
void display();  
void search();  
void main ()  
{  
    int choice =0;  
    while(choice != 9)   
    {  
        printf("\n\n*********Main Menu*********\n");  
        printf("\nChoose one option from the following list ...\n");  
        printf("\n===============================================\n");  
        printf("\n1.Insert in begining\n2.Insert at last\n3.Insert at any random location\n4.Delete from Beginning\n  
        5.Delete from last\n6.Delete node after specified location\n7.Search for an element\n8.Show\n9.Exit\n");  
        printf("\nEnter your choice?\n");         
        scanf("\n%d",&choice);  
        switch(choice)  
        {  
            case 1:  
            beginsert();      
            break;  
            case 2:  
            lastinsert();         
            break;  
            case 3:  
            randominsert();       
            break;  
            case 4:  
            begin_delete();       
            break;  
            case 5:  
            last_delete();        
            break;  
            case 6:  
            random_delete();          
            break;  
            case 7:  
            search();         
            break;  
            case 8:  
            display();        
            break;  
            case 9:  
            exit(0);  
            break;  
            default:  
            printf("Please enter valid choice..");  
        }  
    }  
}  
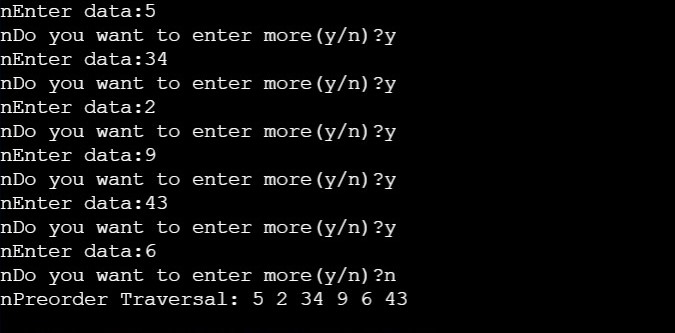
void beginsert()  
{  
    struct node *ptr;  
    int item;  
    ptr = (struct node *) malloc(sizeof(struct node *));  
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW");  
    }  
    else  
    {  
        printf("\nEnter value\n");    
        scanf("%d",&item);    
        ptr->data = item;  
        ptr->next = head;  
        head = ptr;  
        printf("\nNode inserted");  
    }  
      
}  
void lastinsert()  
{  
    struct node *ptr,*temp;  
    int item;     
    ptr = (struct node*)malloc(sizeof(struct node));      
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW");     
    }  
    else  
    {  
        printf("\nEnter value?\n");  
        scanf("%d",&item);  
        ptr->data = item;  
        if(head == NULL)  
        {  
            ptr -> next = NULL;  
            head = ptr;  
            printf("\nNode inserted");  
        }  
        else  
        {  
            temp = head;  
            while (temp -> next != NULL)  
            {  
                temp = temp -> next;  
            }  
            temp->next = ptr;  
            ptr->next = NULL;  
            printf("\nNode inserted");  
          
        }  
    }  
}  
void randominsert()  
{  
    int i,loc,item;   
    struct node *ptr, *temp;  
    ptr = (struct node *) malloc (sizeof(struct node));  
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW");  
    }  
    else  
    {  
        printf("\nEnter element value");  
        scanf("%d",&item);  
        ptr->data = item;  
        printf("\nEnter the location after which you want to insert ");  
        scanf("\n%d",&loc);  
        temp=head;  
        for(i=0;i< loc;i++)  
        {  
            temp = temp->next;  
            if(temp == NULL)  
            {  
                printf("\ncan't insert\n");  
                return;  
            }  
          
        }  
        ptr ->next = temp ->next;   
        temp ->next = ptr;   
        printf("\nNode inserted");  
    }  
}  
void begin_delete()  
{  
    struct node *ptr;  
    if(head == NULL)  
    {  
        printf("\nList is empty\n");  
    }  
    else   
    {  
        ptr = head;  
        head = ptr->next;  
        free(ptr);  
        printf("\nNode deleted from the begining ...\n");  
    }  
}  
void last_delete()  
{  
    struct node *ptr,*ptr1;  
    if(head == NULL)  
    {  
        printf("\nlist is empty");  
    }  
    else if(head -> next == NULL)  
    {  
        head = NULL;  
        free(head);  
        printf("\nOnly node of the list deleted ...\n");  
    }  
          
    else  
    {  
        ptr = head;   
        while(ptr->next != NULL)  
        {  
            ptr1 = ptr;  
            ptr = ptr ->next;  
        }  
        ptr1->next = NULL;  
        free(ptr);  
        printf("\nDeleted Node from the last ...\n");  
    }     
}  
void random_delete()  
{  
    struct node *ptr,*ptr1;  
    int loc,i;    
    printf("\n Enter the location of the node after which you want to perform deletion \n");  
    scanf("%d",&loc);  
    ptr=head;  
    for(i=0;i< loc;i++)  
    {  
        ptr1 = ptr;       
        ptr = ptr->next;  
              
        if(ptr == NULL)  
        {  
            printf("\nCan't delete");  
            return;  
        }  
    }  
    ptr1 ->next = ptr ->next;  
    free(ptr);  
    printf("\nDeleted node %d ",loc+1);  
}  
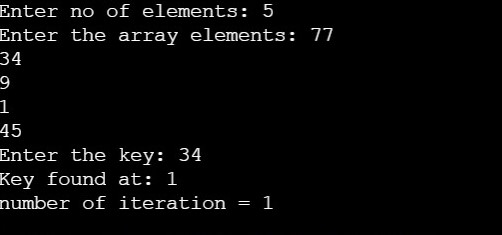
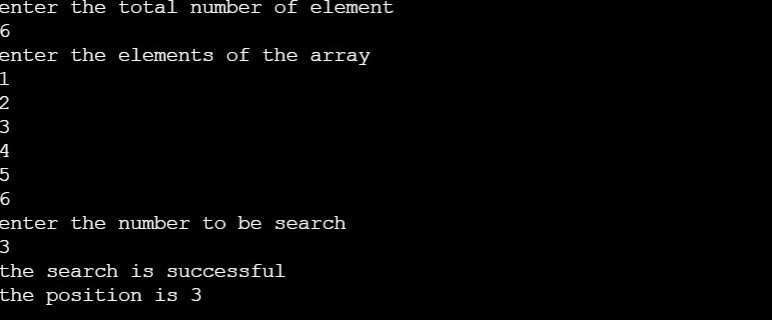
void search()  
{  
    struct node *ptr;  
    int item,i=0,flag;  
    ptr = head;   
    if(ptr == NULL)  
    {  
        printf("\nEmpty List\n");  
    }  
    else  
    {   
        printf("\nEnter item which you want to search?\n");   
        scanf("%d",&item);  
        while (ptr!=NULL)  
        {  
            if(ptr->data == item)  
            {  
                printf("item found at location %d ",i+1);  
                flag=0;  
            }   
            else  
            {  
                flag=1;  
            }  
            i++;  
            ptr = ptr -> next;  
        }  
        if(flag==1)  
        {  
            printf("Item not found\n");  
        }  
    }     
          
}  
  
void display()  
{  
    struct node *ptr;  
    ptr = head;   
    if(ptr == NULL)  
    {  
        printf("Nothing to print");  
    }  
    else  
    {  
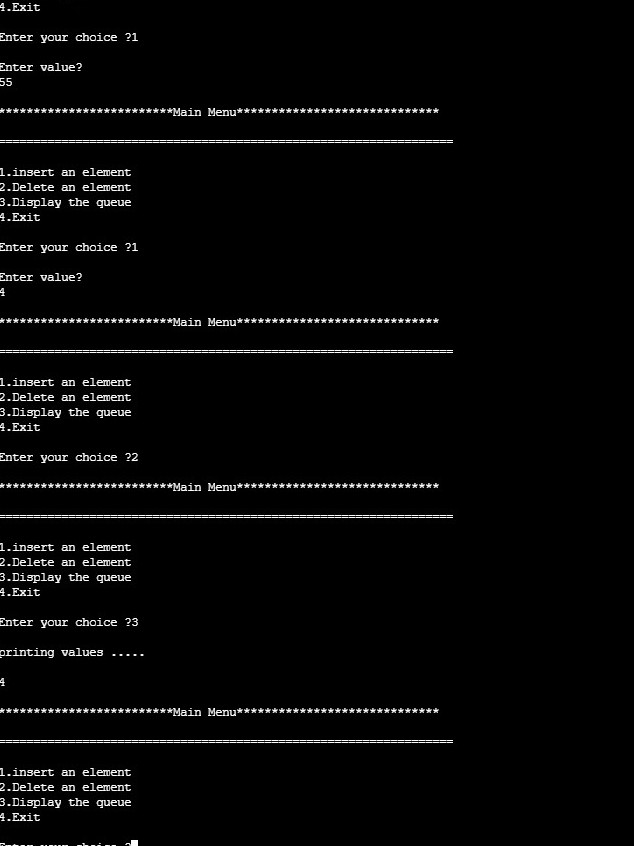
        printf("\nprinting values . . . . .\n");   
        while (ptr!=NULL)  
        {  
            printf("\n%d",ptr->data);  
            ptr = ptr -> next;  
        }  
    }  
}     
                
  

EXPLANATION

TIME COMPLEXITY

Indexing - O(n)
Insertion - O(1)
Search - O(n)
​Deletion - O(1)
                 
                
               

OUTPUT

ALGORITHM

i. Insert At Beginning

Start
Input the DATA to be inserted
Create a new node.
NewNode → Data = DATA NewNode →Lpoint =NULL

IF START IS NULL NewNode→ Rpoint = NULL

Else NewNode → Rpoint = START START→Lpoint = NewNode
START =NewNode
Stop
ii. Insertion at location:

Start
Input the DATA and POS
Initialize TEMP = START; i = 0
Repeat the step 4 if (i less than POS) and (TEMP is not equal to NULL)
TEMP = TEMP → RPoint; i = i +1
If (TEMP not equal to NULL) and (i equal to POS)
(a) Create a New Node

(b) NewNode → DATA = DATA

(c) NewNode → RPoint = TEMP → RPoint

(d) NewNode → LPoint = TEMP

(e) (TEMP → RPoint) → LPoint = NewNode

(f ) TEMP → RPoint = New Node

Else

(a) Display “Position NOT found”

Stop
iii. Insert at End

Start
Input DATA to be inserted
Create a NewNode
NewNode → DATA = DATA
NewNode → RPoint = NULL
If (SATRT equal to NULL)
a. START = NewNode

b. NewNode → LPoint=NULL

Else
a. TEMP = START

b. While (TEMP → Next not equal to NULL)

i. TEMP = TEMP → Next

c. TEMP → RPoint = NewNode

d. NewNode → LPoint = TEMP

Stop
iv. Forward Traversal

Start
If (START is equal to NULL)
a) Display “The list is Empty”

b) Stop

Initialize TEMP = START
Repeat the step 5 and 6 until (TEMP == NULL )
Display “TEMP → DATA”
TEMP = TEMP → Next
Stop
v. Backward Traversal

Start
If (START is equal to NULL)
Display “The list is Empty”
Stop
Initialize TEMP = TAIL
Repeat the step 5 and 6 until (TEMP == NULL )
Display “TEMP → DATA”
TEMP = TEMP → Prev
Stop

            
          

CODE

#include<stdio.h>  
#include<stdlib.h>  
struct node  
{  
    struct node *prev;  
    struct node *next;  
    int data;  
};  
struct node *head;  
void insertion_beginning();  
void insertion_last();  
void insertion_specified();  
void deletion_beginning();  
void deletion_last();  
void deletion_specified();  
void display();  
void search();  
void main ()  
{  
int choice =0;  
    while(choice != 9)  
    {  
        printf("\n*********Main Menu*********\n");  
        printf("\nChoose one option from the following list ...\n");  
        printf("\n===============================================\n");  
        printf("\n1.Insert in begining\n2.Insert at last\n3.Insert at any random location\n4.Delete from Beginning\n  
        5.Delete from last\n6.Delete the node after the given data\n7.Search\n8.Show\n9.Exit\n");  
        printf("\nEnter your choice?\n");  
        scanf("\n%d",&choice);  
        switch(choice)  
        {  
            case 1:  
            insertion_beginning();  
            break;  
            case 2:  
                    insertion_last();  
            break;  
            case 3:  
            insertion_specified();  
            break;  
            case 4:  
            deletion_beginning();  
            break;  
            case 5:  
            deletion_last();  
            break;  
            case 6:  
            deletion_specified();  
            break;  
            case 7:  
            search();  
            break;  
            case 8:  
            display();  
            break;  
            case 9:  
            exit(0);  
            break;  
            default:  
            printf("Please enter valid choice..");  
        }  
    }  
}  
void insertion_beginning()  
{  
    struct node *ptr;   
    int item;  
    ptr = (struct node *)malloc(sizeof(struct node));  
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW");  
    }  
    else  
    {  
    printf("\nEnter Item value");  
    scanf("%d",&item);  
      
    if(head==NULL)  
    {  
        ptr->next = NULL;  
        ptr->prev=NULL;  
        ptr->data=item;  
        head=ptr;  
    }  
    else   
    {  
        ptr->data=item;  
        ptr->prev=NULL;  
        ptr->next = head;  
        head->prev=ptr;  
        head=ptr;  
    }  
    printf("\nNode inserted\n");  
}  
      
}  
void insertion_last()  
{  
    struct node *ptr,*temp;  
    int item;  
    ptr = (struct node *) malloc(sizeof(struct node));  
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW");  
    }  
    else  
    {  
        printf("\nEnter value");  
        scanf("%d",&item);  
        ptr->data=item;  
        if(head == NULL)  
        {  
            ptr->next = NULL;  
            ptr->prev = NULL;  
            head = ptr;  
        }  
        else  
        {  
          temp = head;  
          while(temp->next!=NULL)  
          {  
              temp = temp->next;  
          }  
          temp->next = ptr;  
          ptr ->prev=temp;  
          ptr->next = NULL;  
          }  
              
        }  
      printf("\nnode inserted\n");  
    }  
void insertion_specified()  
{  
    struct node *ptr,*temp;  
    int item,loc,i;  
    ptr = (struct node *)malloc(sizeof(struct node));  
    if(ptr == NULL)  
    {  
        printf("\n OVERFLOW");  
    }  
    else  
    {  
        temp=head;  
        printf("Enter the location");  
        scanf("%d",&loc);  
        for(i=0;i< loc;i++)  
        {  
            temp = temp->next;  
            if(temp == NULL)  
            {  
                printf("\n There are less than %d elements", loc);  
                return;  
            }  
        }  
        printf("Enter value");  
        scanf("%d",&item);  
        ptr->data = item;  
        ptr->next = temp->next;  
        ptr -> prev = temp;  
        temp->next = ptr;  
        temp->next->prev=ptr;  
        printf("\nnode inserted\n");  
    }  
}  
void deletion_beginning()  
{  
    struct node *ptr;  
    if(head == NULL)  
    {  
        printf("\n UNDERFLOW");  
    }  
    else if(head->next == NULL)  
    {  
        head = NULL;   
        free(head);  
        printf("\nnode deleted\n");  
    }  
    else  
    {  
        ptr = head;  
        head = head -> next;  
        head -> prev = NULL;  
        free(ptr);  
        printf("\nnode deleted\n");  
    }  
  
}  
void deletion_last()  
{  
    struct node *ptr;  
    if(head == NULL)  
    {  
        printf("\n UNDERFLOW");  
    }  
    else if(head->next == NULL)  
    {  
        head = NULL;   
        free(head);   
        printf("\nnode deleted\n");  
    }  
    else   
    {  
        ptr = head;   
        if(ptr->next != NULL)  
        {  
            ptr = ptr -> next;   
        }  
        ptr -> prev -> next = NULL;   
        free(ptr);  
        printf("\nnode deleted\n");  
    }  
}  
void deletion_specified()  
{  
    struct node *ptr, *temp;  
    int val;  
    printf("\n Enter the data after which the node is to be deleted : ");  
    scanf("%d", &val);  
    ptr = head;  
    while(ptr -> data != val)  
    ptr = ptr -> next;  
    if(ptr -> next == NULL)  
    {  
        printf("\nCan't delete\n");  
    }  
    else if(ptr -> next -> next == NULL)  
    {  
        ptr ->next = NULL;  
    }  
    else  
    {   
        temp = ptr -> next;  
        ptr -> next = temp -> next;  
        temp -> next -> prev = ptr;  
        free(temp);  
        printf("\nnode deleted\n");  
    }     
}  
void display()  
{  
    struct node *ptr;  
    printf("\n printing values...\n");  
    ptr = head;  
    while(ptr != NULL)  
    {  
        printf("%d\n",ptr->data);  
        ptr=ptr->next;  
    }  
}   
void search()  
{  
    struct node *ptr;  
    int item,i=0,flag;  
    ptr = head;   
    if(ptr == NULL)  
    {  
        printf("\nEmpty List\n");  
    }  
    else  
    {   
        printf("\nEnter item which you want to search?\n");   
        scanf("%d",&item);  
        while (ptr!=NULL)  
        {  
            if(ptr->data == item)  
            {  
                printf("\nitem found at location %d ",i+1);  
                flag=0;  
                break;  
            }   
            else  
            {  
                flag=1;  
            }  
            i++;  
            ptr = ptr -> next;  
        }  
        if(flag==1)  
        {  
            printf("\nItem not found\n");  
        }  
    }     
          
}  
  

TIME COMPLEXITY

Operation                  Time Complexity: Worst Case        Time Complexity: Average Case

Insert at beginning or end                O(1)                              O(1)

Delete at beginning or end                O(1)                              O(1)

Search                                    O(n)                              O(n)

Access                                    O(n)                              O(n)

EXPLANATION

OUTPUT

ALGORITHM

  Step 1 - Include all the header files which are used in the program and define a constant 'SIZE' with specific value.
  Step 2 - Declare all the user defined functions which are used in queue implementation.
  Step 3 - Create a one dimensional array with above defined SIZE (int queue[SIZE])
  Step 4 - Define two integer variables 'front' and 'rear' and initialize both with '-1'. (int front = -1, rear = -1)
  Step 5 - Then implement main method by displaying menu of operations list and make suitable function calls to peroperation selected by the user on queue.
          

CODE

#include <stdio.h>

#define MAX 50
  
void insert();
void delete();
void display();
int queue_array[MAX];
int rear = - 1;
int front = - 1;
main()
{
    int choice;
    while (1)
    {
        printf("1.Insert element to queue \n");
        printf("2.Delete element from queue \n");
        printf("3.Display all elements of queue \n");
        printf("4.Quit \n");
        printf("Enter your choice : ");
        scanf("%d", &choice);
        switch (choice)
        {
            case 1:
            insert();
            break;
            case 2:
            delete();
            break;
            case 3:
            display();
            break;
            case 4:
            exit(1);
            default:
            printf("Wrong choice \n");
        } /* End of switch */
    } /* End of while */
} /* End of main() */
  
void insert()
{
    int add_item;
    if (rear == MAX - 1)
    printf("Queue Overflow \n");
    else
    {
        if (front == - 1)
        /*If queue is initially empty */
        front = 0;
        printf("Inset the element in queue : ");
        scanf("%d", &add_item);
        rear = rear + 1;
        queue_array[rear] = add_item;
    }
} /* End of insert() */
  
void delete()
{
    if (front == - 1 || front > rear)
    {
        printf("Queue Underflow \n");
        return ;
    }
    else
    {
        printf("Element deleted from queue is : %d\n", queue_array[front]);
        front = front + 1;
    }
} /* End of delete() */
  
void display()
{
    int i;
    if (front == - 1)
        printf("Queue is empty \n");
    else
    {
        printf("Queue is : \n");
        for (i = front; i <= rear; i++)
            printf("%d ", queue_array[i]);
        printf("\n");
    }
}
  

TIME COMPLEXITY

    Enqueue Time Complexity: O(1) 
    Dequeue Time Complexity: O(1) 
    Display Time Complexity: O(n) 

EXPLANATION

OUTPUT

ALGORITHM

    
Algorithm Enqueue
    newNode -> data = data
    newNode -> next = NULL
    if ( REAR == NULL)
    FRONT = REAR = newNode
    end if
    else
    REAR -> next = newNode
    REAR = newNode
    end Algorithm_Enqueue
    
Algorithm Dequeue
    if(FRONT == NULL)
    print "EMPTY QUEUE" and exit.
    end if
    end Algorithm_Dequeue
    else
    temp = FRONT
    FRONT = FRONT -> NEXT
    free(temp)
    end else
    end Algorithm_Dequeue
            

CODE

#include<stdio.h>   
#include<stdlib.h>  
struct node   
{  
    int data;   
    struct node *next;  
};  
struct node *front;  
struct node *rear;   
void insert();  
void delete();  
void display();  
void main ()  
{  
    int choice;   
    while(choice != 4)   
    {     
        printf("\n*************************Main Menu*****************************\n");  
        printf("\n=================================================================\n");  
        printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");  
        printf("\nEnter your choice ?");  
        scanf("%d",& choice);  
        switch(choice)  
        {  
            case 1:  
            insert();  
            break;  
            case 2:  
            delete();  
            break;  
            case 3:  
            display();  
            break;  
            case 4:  
            exit(0);  
            break;  
            default:   
            printf("\nEnter valid choice??\n");  
        }  
    }  
}  
void insert()  
{  
    struct node *ptr;  
    int item;   
      
    ptr = (struct node *) malloc (sizeof(struct node));  
    if(ptr == NULL)  
    {  
        printf("\nOVERFLOW\n");  
        return;  
    }  
    else  
    {   
        printf("\nEnter value?\n");  
        scanf("%d",&item);  
        ptr -> data = item;  
        if(front == NULL)  
        {  
            front = ptr;  
            rear = ptr;   
            front -> next = NULL;  
            rear -> next = NULL;  
        }  
        else   
        {  
            rear -> next = ptr;  
            rear = ptr;  
            rear->next = NULL;  
        }  
    }  
}     
void delete ()  
{  
    struct node *ptr;  
    if(front == NULL)  
    {  
        printf("\nUNDERFLOW\n");  
        return;  
    }  
    else   
    {  
        ptr = front;  
        front = front -> next;  
        free(ptr);  
    }  
}  
void display()  
{  
    struct node *ptr;  
    ptr = front;      
    if(front == NULL)  
    {  
        printf("\nEmpty queue\n");  
    }  
    else  
    {   printf("\nprinting values .....\n");  
        while(ptr != NULL)   
        {  
            printf("\n%d\n",ptr -> data);  
            ptr = ptr -> next;  
        }  
    }  
}   
  

TIME COMPLEXITY

    Enqueue Time Complexity: O(1) 
    Dequeue Time Complexity: O(1) 
    Display Time Complexity: O(n) 

EXPLANATION

OUTPUT

ALGORITHM

  
Algorithm Enqueue
  Step 1: IF (REAR+1)%MAX = FRONT
  Write " OVERFLOW "
  Goto step 4
  [End OF IF]
  
  Step 2: IF FRONT = -1 and REAR = -1
  SET FRONT = REAR = 0
  ELSE IF REAR = MAX - 1 and FRONT ! = 0
  SET REAR = 0
  ELSE
  SET REAR = (REAR + 1) % MAX
  [END OF IF]
  
  Step 3: SET QUEUE[REAR] = VAL
  
Algorithm Dequeue
  Step 1: IF FRONT = -1
Write " UNDERFLOW "
Goto Step 4
  [END of IF]
Step 2: SET VAL = QUEUE[FRONT]
Step 3: IF FRONT = REAR
SET FRONT = REAR = -1
  ELSE
IF FRONT = MAX -1
SET FRONT = 0
  ELSE
SET FRONT = FRONT + 1
  [END of IF]
  [END OF IF]
Step 4: EXIT
          

CODE

#include <stdio.h>
#define size 5

void insertq(int[], int);
void deleteq(int[]);
void display(int[]);

int front =  - 1;
int rear =  - 1;

int main()
{
    int n, ch;
    int queue[size];
    do
    {
        printf("\n\n Circular Queue:\n1. Insert \n2. Delete\n3. Display\n0. Exit");
        printf("\nEnter Choice 0-3? : ");
        scanf("%d", &ch);
        switch (ch)
        {
            case 1:
                printf("\nEnter number: ");
                scanf("%d", &n);
                insertq(queue, n);
                break;
            case 2:
                deleteq(queue);
                break;
            case 3:
                display(queue);
                break;
        }
    }while (ch != 0);
}


void insertq(int queue[], int item)
{
    if ((front == 0 && rear == size - 1) || (front == rear + 1))
    {
        printf("queue is full");
        return;
    }
    else if (rear ==  - 1)
    {
        rear++;
        front++;
    }
    else if (rear == size - 1 && front > 0)
    {
        rear = 0;
    }
    else
    {
        rear++;
    }
    queue[rear] = item;
}

void display(int queue[])
{
    int i;
    printf("\n");
    if (front > rear)
    {
        for (i = front; i < size; i++)
        {
            printf("%d ", queue[i]);
        }
        for (i = 0; i <= rear; i++)
            printf("%d ", queue[i]);
    }
    else
    {
        for (i = front; i <= rear; i++)
            printf("%d ", queue[i]);
    }
}

void deleteq(int queue[])
{
    if (front ==  - 1)
    {
        printf("Queue is empty ");
    }
    else if (front == rear)
    {
        printf("\n %d deleted", queue[front]);
        front =  - 1;
        rear =  - 1;
    }
    else
    {
        printf("\n %d deleted", queue[front]);
        front++;
    }
}  
  

TIME COMPLEXITY

    Enqueue Time Complexity: O(1) 
    Dequeue Time Complexity: O(1) 
    Display Time Complexity: O(n) 

EXPLANATION

OUTPUT

ALGORITHM

  START
      Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
  END IF
   
END Procedure
STOP
  

CODE

#include <stdio.h>

void towers(int, char, char, char);
  
int main()
{
    int num;
  
    printf("Enter the number of disks : ");
    scanf("%d", &num);
    printf("The sequence of moves involved in the Tower of Hanoi are :\n");
    towers(num, 'A', 'C', 'B');
    return 0;
}
void towers(int num, char frompeg, char topeg, char auxpeg)
{
    if (num == 1)
    {
        printf("\n Move disk 1 from peg %c to peg %c", frompeg, topeg);
        return;
    }
    towers(num - 1, frompeg, auxpeg, topeg);
    printf("\n Move disk %d from peg %c to peg %c", num, frompeg, topeg);
    towers(num - 1, auxpeg, topeg, frompeg);
}   
  

TIME COMPLEXITY

Time Complexity of Tower of Hanoi = O(2^n)

EXPLANATION

OUTPUT

ALGORITHM

  Input matrix 1 and matrix 2.
  If the number of rows and number of columns of matrix 1 and matrix 2 is equal,
  for i=1 to rows[matrix 1]
  for j=1 to columns [matrix 1]
  Input matrix 1 [i,j]
  Input matrix 2 [i,j]
  matrix 3 [i,j]= matrix 1 [i,j]+ matrix 2 [i,j];
  Display matrix 3 [i,j];
          

CODE

#include <stdio.h>

int main()
{
    int m, n, c, d, first[10][10], second[10][10], sum[10][10];
  
    printf("Enter the number of rows and columns of matrix\n");
    scanf("%d%d", &m, &n);
    printf("Enter the elements of first matrix\n");
  
    for (c = 0; c < m; c++)
      for (d = 0; d < n; d++)
          scanf("%d", &first[c][d]);
  
    printf("Enter the elements of second matrix\n");
  
    for (c = 0; c < m; c++)
      for (d = 0 ; d < n; d++)
          scanf("%d", &second[c][d]);
    
    printf("Sum of entered matrices:-\n");
    
    for (c = 0; c < m; c++) {
      for (d = 0 ; d < n; d++) {
          sum[c][d] = first[c][d] + second[c][d];
          printf("%d\t", sum[c][d]);
      }
      printf("\n");
    }
  
    return 0;
}  
  

TIME COMPLEXITY

Time Complexity of Matrix Transpose = O(n^2)

EXPLANATION

OUTPUT

ALGORITHM

  Step 1: Start the Program.

  Step 2: Enter the row and column of the first (a) matrix.

  Step 3: Enter the row and column of the second (b) matrix.

  Step 4: Enter the elements of the first (a) matrix.

  Step 5: Enter the elements of the second (b) matrix.

  Step 6: Print the elements of the first (a) matrix in matrix form.
          

CODE

#include<stdio.h>    
#include<stdlib.h>  
int main(){  
int a[10][10],b[10][10],mul[10][10],r,c,i,j,k;    
system("cls");  
printf("enter the number of row=");    
scanf("%d",&r);    
printf("enter the number of column=");    
scanf("%d",&c);    
printf("enter the first matrix element=\n");    
for(i=0;i< r;i++)    
{    
for(j=0;j< c;j++)    
{    
scanf("%d",&a[i][j]);    
}    
}    
printf("enter the second matrix element=\n");    
for(i=0;i< r;i++)    
{    
for(j=0;j< c;j++)    
{    
scanf("%d",&b[i][j]);    
}    
}    
    
printf("multiply of the matrix=\n");    
for(i=0;i< r;i++)    
{    
for(j=0;j< c;j++)    
{    
mul[i][j]=0;    
for(k=0;k< c;k++)    
{    
mul[i][j]+=a[i][k]*b[k][j];    
}    
}    
}    
//for printing result    
for(i=0;i< r;i++)    
{    
for(j=0;j< c;j++)    
{    
printf("%d\t",mul[i][j]);    
}    
printf("\n");    
}    
return 0;  
}  
                   
  

TIME COMPLEXITY

Time Complexity of Matrix Transpose = O(n*n*n) , where n is the size of the matrix.

EXPLANATION

OUTPUT

ALGORITHM

  We first declare two matrices a and b of order mxn

  Then we read matrix a from the user. We will use matrix b to store transpose of the matrix.

  Now, we declare two variables i, j and initialize them to 0

  After this we start a loop of i, till it reaches n which gave us the column indexes and inside it a loop of j which gives us the elements of the row.
          

CODE

#include <stdio.h>

int main()
{
  int m, n, c, d, matrix[10][10], transpose[10][10];
  
  printf("Enter the number of rows and columns of a matrix\n");
  scanf("%d%d", &m, &n);
  printf("Enter elements of the matrix\n");
  
  for (c = 0; c < m; c++)
    for (d = 0; d < n; d++)
      scanf("%d", &matrix[c][d]);
  
  for (c = 0; c < m; c++)
    for (d = 0; d < n; d++)
      transpose[d][c] = matrix[c][d];
  
  printf("Transpose of the matrix:\n");
  
  for (c = 0; c < n; c++) {
    for (d = 0; d < m; d++)
      printf("%d\t", transpose[c][d]);
    printf("\n");
  }

  return 0;
}    
  

TIME COMPLEXITY

Time Complexity of Matrix Transpose = O(m*n) , where m and n are the row and column of the matrix.

EXPLANATION

OUTPUT

ALGORITHM

  bubbleSort(array)
    for i <- 1 to indexOfLastUnsortedElement-1
      if leftElement > rightElement
        swap leftElement and rightElement
  end bubbleSort
          

CODE

#include<stdio.h>
int main()
{
int arr[10],n,i,round,temp;
printf("enter the number of elements in array\n");
scanf("%d",&n);
printf("enter the elements\n");
for(i=0;i< n;i++)
{
scanf("%d",&arr[i]);
}
for(round=1;round< n;round++)
    for(i=0;i< n-round;i++)
    if(arr[i]>arr[i+1])
{
    temp=arr[i];
    arr[i]=arr[i+1];
    arr[i+1]=temp;
}
printf("the sorted array\n");
for(i=0;i< n;i++)
{
    printf("  %d",arr[i]);
}
}
                            
  

TIME COMPLEXITY

  Worst Case Complexity = O(n^2)
  Best Case Complexity = O(n)
  Average Case Complexity = O(n^2)
  

EXPLANATION

OUTPUT

ALGORITHM

  insertionSort(array)

  mark first element as sorted

  for each unsorted element X

    'extract' the element X

    for j <- lastSortedIndex down to 0

      if current element j > X

        move sorted element to the right by 1

    break loop and insert X here

  end insertionSort
          

CODE

#include<stdio.h>
void insertion_sort(int arr[], int n);
int main()
{
int arr[100], i,n;
printf("enter the number of elements\n");
scanf("%d",&n);
printf("enter the elements\n");
for(i=0;i< n;i++)
{
scanf("%d",&arr[i]);
}
insertion_sort(arr , n);
printf("the sorted array is\n");
for(i=0;i< n;i++)
printf(" %d",arr[i]);
}
void insertion_sort(int arr[], int n)
{
int i,j,temp;
for(i=1;i< n;i++)
{
temp = arr[i];
j=i-1;
while((temp< arr[j]) && j>=0)
{
arr[j+1]=arr[j];
j--;
}
arr[j+1]=temp;
}
}
                            
  

TIME COMPLEXITY

Worst Case Complexity = O(n^2)
Best Case Complexity = O(n)
Average Case Complexity = O(n^2)

EXPLANATION

OUTPUT

ALGORITHM

  selectionSort(array, size)

    repeat (size - 1) times

    set the first unsorted element as the minimum

    for each of the unsorted elements

      if element < currentMinimum

        set element as new minimum

    swap minimum with first unsorted position

  end selectionSort
          

CODE

#include<stdio.h>
int selection_sort(int n,int arr[])
{
  int i,j,min,temp;
  for(i=0;i< n-1;i++)
  {
    min=i;
    for(j=i+1;j< n;j++)
    {
      if(arr[j]< arr[min])
      min=j;
    }
    temp=arr[i];
    arr[i]=arr[min];
    arr[min]=temp;
  }
  result(n,arr);
}
int result(int n,int arr[])
{
  int i;
  printf("The sorted array is: \n");
  for(i=0;i< n;i++)
  {
    printf("%d ",arr[i]);
  }
}
int main()
{
  int n,i;
  printf("Enter the number of elements in the array: ");
  scanf("%d",&n);
  int arr[n];
  printf("Enter the elements in the array: \n");
  for(i=0;i< n;i++)
  {
    scanf("%d",&arr[i]);
  }
  selection_sort(n,arr);
}
                           
  

EXPLANATION

OUTPUT

ALGORITHM

  MergeSort(arr[], l,  r)
    If r > l
       Find the middle point to divide the array into two halves:  
              middle m = l+ (r-l)/2

       Call mergeSort for first half:   
              Call mergeSort(arr, l, m)

       Call mergeSort for second half:
              Call mergeSort(arr, m+1, r)

       Merge the two halves sorted in step 2 and 3:
              Call merge(arr, l, m, r)
          

CODE

#include<stdio.h>
void mergesort(int a[],int i,int j);
void merge(int a[],int i1,int j1,int i2,int j2);

int main()
{
int a[30],n,i;
printf("Enter no of elements:");
scanf("%d",&n);
printf("Enter array elements:");

for(i=0;i< n;i++)
  scanf("%d",&a[i]);

mergesort(a,0,n-1);

printf("\nSorted array is :");
for(i=0;i< n;i++)
  printf("%d ",a[i]);

return 0;
}

void mergesort(int a[],int i,int j)
{
int mid;

if(i< j)
{
  mid=(i+j)/2;
  mergesort(a,i,mid);		//left recursion
  mergesort(a,mid+1,j);	//right recursion
  merge(a,i,mid,mid+1,j);	//merging of two sorted sub-arrays
}
}

void merge(int a[],int i1,int j1,int i2,int j2)
{
int temp[50];	//array used for merging
int i,j,k;
i=i1;	//beginning of the first list
j=i2;	//beginning of the second list
k=0;

while(i<=j1 && j<=j2)	//while elements in both lists
{
  if(a[i]< a[j])
    temp[k++]=a[i++];
  else
    temp[k++]=a[j++];
}

while(i<=j1)	//copy remaining elements of the first list
  temp[k++]=a[i++];

while(j<=j2)	//copy remaining elements of the second list
  temp[k++]=a[j++];

//Transfer elements from temp[] back to a[]
for(i=i1,j=0;i<=j2;i++,j++)
  a[i]=temp[j];
}

                
                            
  

TIME COMPLEXITY

  Worst Case Complexity = O(n logn)
  Best Case Complexity = O(n logn)
  Average Case Complexity = O(n logn)

EXPLANATION

OUTPUT

ALGORITHM

  /* low  --> Starting index,  high  --> Ending index */
  quickSort(arr[], low, high)
  {
      if (low < high)
      {
          /* pi is partitioning index, arr[pi] is now
            at right place */
          pi = partition(arr, low, high);

          quickSort(arr, low, pi - 1);  // Before pi
          quickSort(arr, pi + 1, high); // After pi
      }
  }
          

CODE

#include<stdio.h>
void quicksort(int number[25],int first,int last){
    int i, j, pivot, temp;

    if(first< last){
      pivot=first;
      i=first;
      j=last;

      while(i< j){
          while(number[i]<=number[pivot]&&i< last)
            i++;
          while(number[j]>number[pivot])
            j--;
          if(i< j){
            temp=number[i];
            number[i]=number[j];
            number[j]=temp;
          }
      }

      temp=number[pivot];
      number[pivot]=number[j];
      number[j]=temp;
      quicksort(number,first,j-1);
      quicksort(number,j+1,last);

    }
}

int main(){
    int i, count, number[25];

    printf("How many elements are u going to enter?: ");
    scanf("%d",&count);

    printf("Enter %d elements: ", count);
    for(i=0;i< count;i++)
      scanf("%d",&number[i]);

    quicksort(number,0,count-1);

    printf("Order of Sorted elements: ");
    for(i=0;i< count;i++)
      printf(" %d",number[i]);

    return 0;
}
                           
  

TIME COMPLEXITY

  Worst Case Complexity = O(n^2)
  Best Case Complexity = O(n logn)
  Average Case Complexity = O(n logn)

EXPLANATION

OUTPUT

ALGORITHM

  Step 1 − Choose the highest index value has pivot

  Step 2 − Take two variables to point left and right of the list excluding pivot

  Step 3 − left points to the low index

  Step 4 − right points to the high

  Step 5 − while value at left is less than pivot move right

  Step 6 − while value at right is greater than pivot move left

  Step 7 − if both step 5 and step 6 does not match swap left and right

  Step 8 − if left ≥ right, the point where they met is new pivot
          

CODE

#include<stdio.h>  
int temp;  
  
void heapify(int arr[], int size, int i)  
{  
int largest = i;    
int left = 2*i + 1;    
int right = 2*i + 2;    
  
if (left < size && arr[left] >arr[largest])  
largest = left;  
  
if (right < size && arr[right] > arr[largest])  
largest = right;  
  
if (largest != i)  
{  
temp = arr[i];  
    arr[i]= arr[largest];   
    arr[largest] = temp;  
heapify(arr, size, largest);  
}  
}  
  
void heapSort(int arr[], int size)  
{  
int i;  
for (i = size / 2 - 1; i >= 0; i--)  
heapify(arr, size, i);  
for (i=size-1; i>=0; i--)  
{  
temp = arr[0];  
    arr[0]= arr[i];   
    arr[i] = temp;  
heapify(arr, i, 0);  
}  
}  
  
void main()  
{  
int arr[] = {1, 10, 2, 3, 4, 1, 2, 100,23, 2};  
int i;  
int size = sizeof(arr)/sizeof(arr[0]);  
  
heapSort(arr, size);  
  
printf("printing sorted elements\n");  
for (i=0; i< size; ++i)  
printf("%d\n",arr[i]);  
}      
  

TIME COMPLEXITY

 Worst case complexity = O(n logn)
 Average case complexity = O(n logn)
 Best case complexity = O(n logn) 

EXPLANATION

OUTPUT

ALGORITHM

  Linear Search ( Array A, Value x)

  Step 1: Set i to 1

  Step 2: if i > n then go to step 7

  Step 3: if A[i] = x then go to step 6

  Step 4: Set i to i + 1

  Step 5: Go to Step 2

  Step 6: Print Element x Found at index i and go to step 8

  Step 7: Print element not found

  Step 8: Exit
          

CODE

#include<stdio.h>
int linear(int ar[],int n,int key)
{
  int i,f=0,pos,c=0;
  for(i=0;i< n;i++)
  {
    if(ar[i]==key)
    {

    pos=i;

    f=1;
    break;

    }
    else
    {
      f=0;
        c++;

    }

  }
  if(f==1)
  {
    printf("Key found at: %d\n",pos);
    printf("number of iteration = %d",c);
      }
  else
  {
    printf("Not found");
  }
}

int main()
{
  int arr[10],i,n,key;
  printf("Enter no of elements: ");
  scanf("%d",&n);
  printf("Enter the array elements: ");
  for(i=0;i< n;i++)
  {
    scanf("%d",&arr[i]);
  }
  printf("Enter the key: ");
  scanf("%d",&key);
  linear(arr,n,key);
}
                             
  

TIME COMPLEXITY

  Worst case time complexity = O(n)           
  Average case time complexity = O(n/2)           
  Best case time complexity = O(1)           
          

EXPLANATION

OUTPUT

ALGORITHM

  BINARY_SEARCH(A, lower_bound, upper_bound, VAL)

  Step 1: [INITIALIZE] SET BEG = lower_bound END = upper_bound, POS = - 1

  Step 2: Repeat Steps 3 and 4 while BEG <=END

  Step 3: SET MID = (BEG + END)/2

  Step 4: IF A[MID] = VAL
  SET POS = MID
  PRINT POS

  Go to Step 6

  ELSE IF A[MID] > VAL
  SET END = MID - 1
  ELSE
  SET BEG = MID + 1
    [END OF IF]
    [END OF LOOP]

  Step 5: IF POS = -1
  PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
  [END OF IF]

  Step 6: EXIT
          

CODE

#include<stdio.h>
  int main()
  {
  int arr[10],i,n,item,loc=0,beg=0,mid,end;
  printf("enter the total number of element\n");
  scanf("%d",&n);
  printf("enter the elements of the array\n");
  for(i=0;i< n;i++)
  {
  scanf("%d",&arr[i]);
  }
  printf("enter the number to be search\n");
  scanf("%d",&item);
  end=n-1;
  while((beg<=end))
  {
  mid=((end+beg)/2);
  if(item==arr[mid])
  {
  printf("the search is successful\n");
  loc=mid+1;
  printf("the position is %d",loc);
  break;
  }
  else if (item< arr[mid])
  end = mid -1;
  else
  beg = mid +1;
  }
  if (loc == 0)
  printf("not found");
  }
                             
  

TIME COMPLEXITY

Best case time complexity = O(1)
Average case time complexity = O(logn)
Worst case time complexity = O(logn)

EXPLANATION

OUTPUT

ALGORITHM

            
SEARCH OPERATION

  Step 1 - Read the search element from the user.

  Step 2 - Compare the search element with the value of root node in the tree.

  Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function

  Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value.

  Step 5 - If search element is smaller, then continue the search process in left subtree.

  Step 6- If search element is larger, then continue the search process in right subtree.

  Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node

  Step 8 - If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function.

  Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.

  
INSERTION OPERATION

    Step 1 - Create a newNode with given value and set its left and right to NULL.

    Step 2 - Check whether tree is Empty.

    Step 3 - If the tree is Empty, then set root to newNode.

    Step 4 - If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node).

    Step 5 - If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child.

    Step 6- Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL).

    Step 7 - After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.
          
  
DELETION OPERATION

  Case 1: Deleting a leaf node

  Step 1 - Find the node to be deleted using search operation
  Step 2 - Delete the node using free function (If it is a leaf) and terminate the function.

  Case 2: Deleting a node with one child
  
  Step 1 - Find the node to be deleted using search operation
  Step 2 - If it has only one child then create a link between its parent node and child node.
  Step 3 - Delete the node using free function and terminate the function.

  Case 3: Deleting a node with two children

  Step 1 - Find the node to be deleted using search operation
  Step 2 - If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree.
  Step 3 - Swap both deleting node and node which is found in the above step.
  Step 4 - Then check whether deleting node came to case 1 or case 2 or else goto step 2
  Step 5 - If it comes to case 1, then delete using case 1 logic.
  Step 6- If it comes to case 2, then delete using case 2 logic.
  Step 7 - Repeat the same process until the node is deleted from the tree.
  

CODE

#include<stdio.h>
#include<stdlib.h>
  
typedef struct BST
{
int data;
struct BST *left;
struct BST *right;
}node;
  
node *create();
void insert(node *,node *);
void preorder(node *);
  
int main()
{
char ch;
node *root=NULL,*temp;
do
{
temp=create();
if(root==NULL)
root=temp;
else
insert(root,temp);
printf("nDo you want to enter more(y/n)?");
getchar();
scanf("%c",&ch);
}while(ch=='y'|ch=='Y');
printf("nPreorder Traversal: ");
preorder(root);
return 0;
}
  
node *create()
{
node *temp;
printf("nEnter data:");
temp=(node*)malloc(sizeof(node));
scanf("%d",&temp->data);
temp->left=temp->right=NULL;
return temp;
}
  
void insert(node *root,node *temp)
{
if(temp->data< root->data)
{
if(root->left!=NULL)
insert(root->left,temp);
else
root->left=temp;
}
if(temp->data>root->data)
{
if(root->right!=NULL)
insert(root->right,temp);
else
root->right=temp;
}
}
  
void preorder(node *root)
{
if(root!=NULL)
{
printf("%d ",root->data);
preorder(root->left);
preorder(root->right);
}
}  
  

TIME COMPLEXITY

SEARCHING = O(n)

INSERTION = O(n)

DELETION = O(n)

EXPLANATION

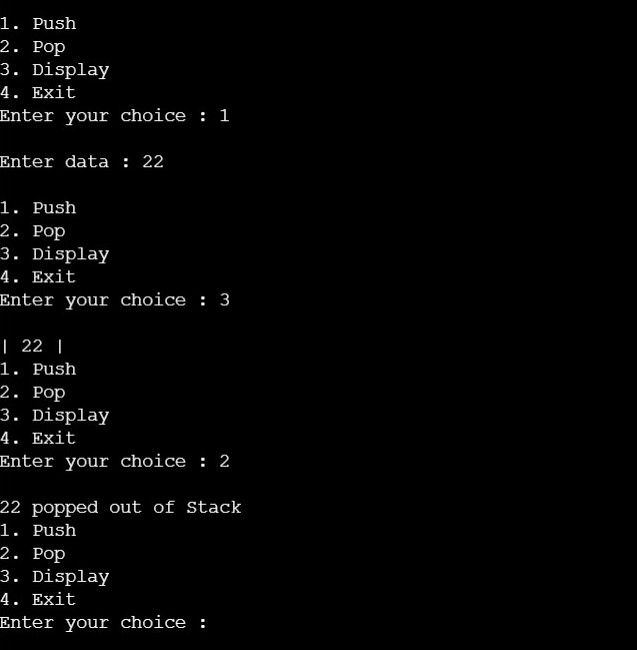
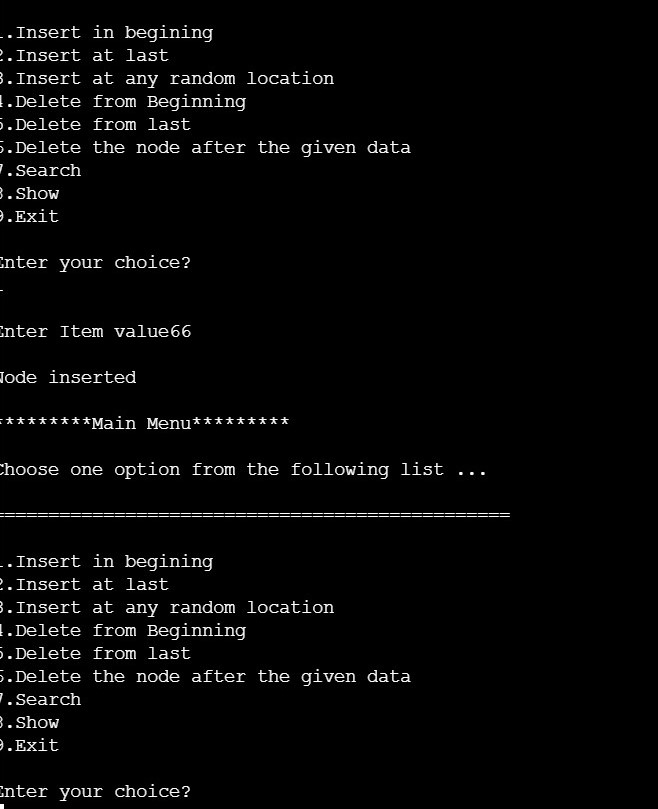
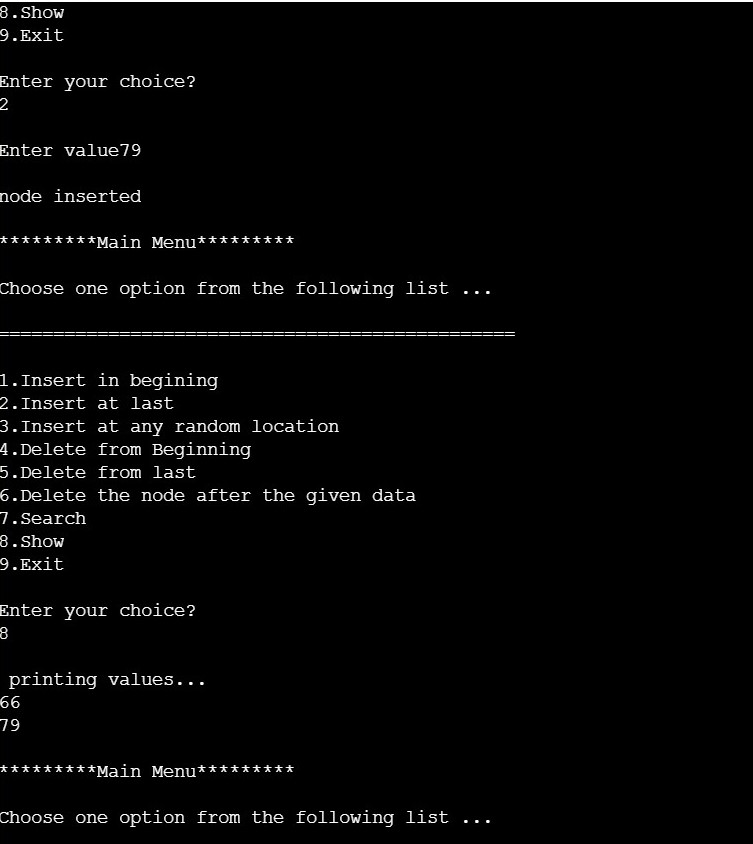
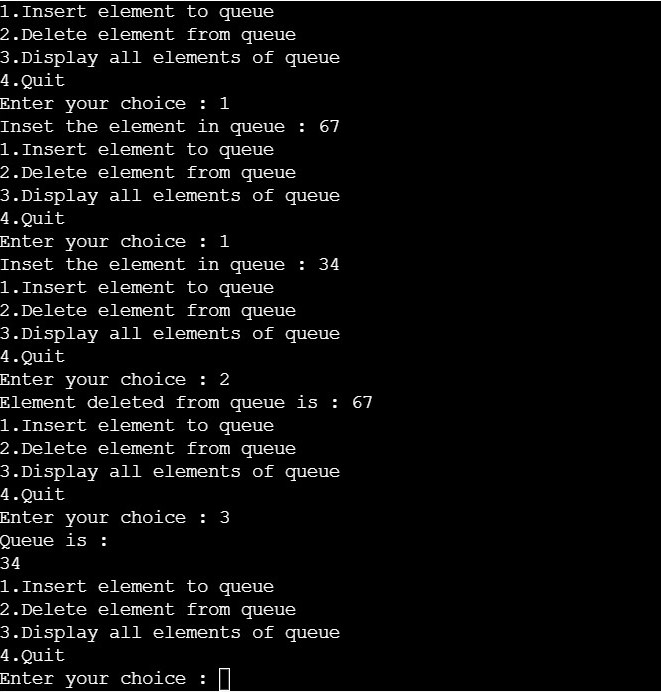
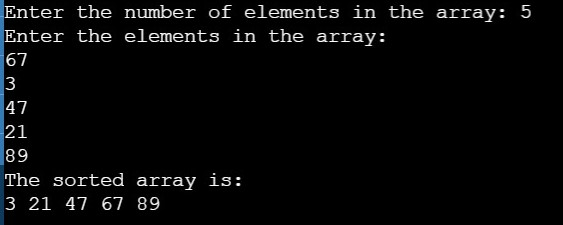
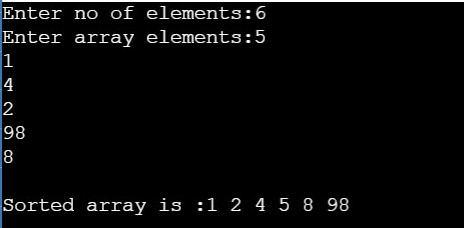
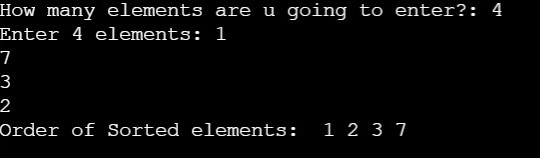
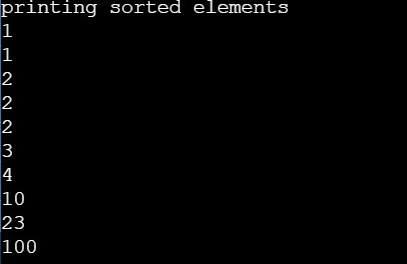
OUTPUT